Enharmonic Intervals Demystified

Different names for the same sound, why?

In this post, we're going to clarify a topic that often confuses many novice guitar players: enharmonic intervals. From a beginner's perspective, enharmonics are tricky because they have different names but the same sounds, how is that possible?

Actually, enharmonic intervals are easier than it seems.

Intervals

Intervals, as we have already seen in our posts about fretboard intervals and chord construction, are simply a distance between two pitches.

An interval has a quality and a quantity.

Interval Quantity

Let's start with the quantity: to determine the quantity of an interval, we simply count how many notes there are between our two pitches,counting the notes of the major scale: C, D, E, F, G, A, B and C.

Some examples:

C to D: 2 notes, this is a Second Interval
C to E: 3 notes, this is a Third Interval
E to G: 3 notes, this is a Third Interval
A to E: 5 notes, this is a Fifth Interval
G to F: 7 notes, this is a Seventh Interval
E to C: 6 notes, this is a Sixth Interval

So, we can now show the complete table of Interval quantities

Name	Count	Example
Unison	0	C to C
Second	2	C to D
Third	3	C to E
Fourth	0	C to F
Fifth	0	C to G
Sixth	6	C to A
Seventh	7	C to B
Octave	8	C to C

Interval Quality

When dealing with interval quantities, we have 7 different options (the 7 notes of the major scale).

But in an octave there are 12 semitones, so we use interval qualities to get more specific.

Here are the possible qualities for an interval

Minor
Major
Perfect
Augmented
Diminished

There are some rules that apply to qualities:

We don't use major and minor qualities with 4th and 5th intervals (that is, major 4th or minor 5th do not exist)
We don't use perfect quality with 2nd, 3rd, 6th and 7th intervals
A minor interval is one half-step smaller than a major interval
An augmented interval is one half-step larger than a perfect interval
A diminished interval is one half-step smaller than a perfect interval

So all the possible combination we can have are:

Minor, Major, Augmented and Diminished Seconds
Minor, Major, Augmented and Diminished Thirds
Perfect, Augmented and Diminished Fourths
Perfect, Augmented and Diminished Fifths
Minor, Major, Augmented and Diminished Sixths
Minor, Major, Augmented and Diminished Sevenths

Here below you find a comprehensive table of interval quantities and qualities

Quality	Interval	Half-Steps	Example
	Unison	0	C to C
Minor	Second	1	C to D#
Major	Second	2	C to D
Minor	Third	3	C to Eb
Major	Third	4	C to E
Perfect	Fourth	5	C to F
Augmented	Fourth	6	C to F#
Diminished	Fifth	6	C to Gb
Perfect	Fifth	7	C to G
Minor	Sixth	8	C to Ab
Major	Sixth	9	C to A
Minor	Seventh	10	C to Bb
Major	Seventh	11	C to B
	Octave	12	C to C

Enharmonic Intervals

In the table above, you can notice that there is an interval 6 half steps wide that is listed as Augmented 4th and Diminished 5th both.

This is an enharmonic. There are the same notes on guitar, but have different names.

The key to deal with enharmonics is to count on interval quality:

Between the intervals C to Eb and C to D# there are 3 half steps, but with a difference:

From C to Eb there are 3 notes, so this is a Third Interval
From C to D# we count 2 notes, so this is a Second Interval

Now let's analyze qualities:

C to Eb is a Minor Third because it's a 3 half-step interval (by looking at the chart above)
C to D# is an Augmented Second, because it's 1 half-step wider than a Major Second

That's is: they are 3 half-steps large both, but with 2 different names because they have different quantities.

An example enharmonics with chords

Let's compare these 2 chords: C Major Sixth and C Diminished Seventh

C Major Sixth

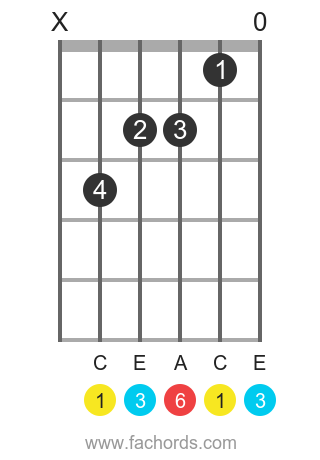
This chord is composed of the Root (C), Major Third (E), Perfect Fifth (G) and Major Sixth (A)

C Diminished Seventh

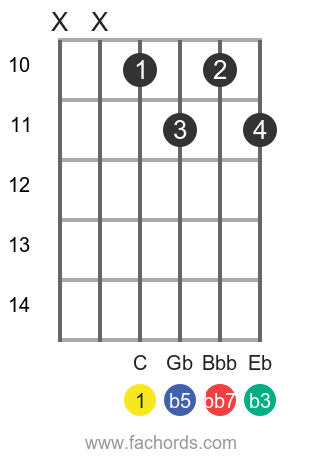
This chord is composed of the Root (C), Minor Third (Eb), Diminished Fifth (Gb) and Diminished Seventh (Bbb)

bb7

Did you spot where the enharmonic is?

The note A in the first chord and the note Bbb in the second chord have exactly the same length, 9 half-steps, but they have different names because of the note involved:

C to A is a Sixth Interval (we count 6 notes), while C to B is a Seventh Interval (7 notes).

You find more examples of chords structure in our online guitar chord library.

Enharmonics - Conclusion

I hope to have clarified a bit what enharmonics are and how they related to intervals qualities.

At the end of the day, it strongly depends on the context in which you're operating: if you're building a seventh chord you'll have a certain set of intervals; in the case of different chord type you'll have a different intervals set.

Stick to the counting notes method (quantity) and your life will be easier.

Click here to stay updated on new tutorials and music learning resources.

FAQ

What are enharmonic intervals and why are they important in music theory for guitarists?

Enharmonic intervals are notes that sound identical because they occupy the same position on the fretboard (same number of half-steps), but they are named differently based on their musical context. They are crucial for guitarists to understand because the naming convention (e.g., F# vs. Gb, or A vs. Bbb) indicates the note's role within a scale or chord, affecting how we analyze and understand harmony.

How can I determine if two intervals are enharmonic?

You can identify enharmonic intervals by noting that they span the same number of half-steps but have different names due to their distinct quantity and quality. For example, an Augmented 4th and a Diminished 5th both cover 6 half-steps. Similarly, a Minor Third (C to Eb) and an Augmented Second (C to D#) both cover 3 half-steps, yet they are named differently because one is a 'Third' and the other a 'Second' in quantity.

What is the difference between an interval's 'quantity' and its 'quality'?

An interval's 'quantity' refers to the number of scale notes (e.g., C-D-E for a third) between two pitches, determining if it's a 2nd, 3rd, 4th, etc. The 'quality' then refines this, describing the exact number of half-steps and giving it a specific characteristic like Minor, Major, Perfect, Augmented, or Diminished. Both are necessary to fully define an interval.

Why don't we use 'Major' or 'Minor' qualities for 4th and 5th intervals, or 'Perfect' for 2nd, 3rd, 6th, and 7th intervals?

In standard music theory, specific quality terms are reserved for certain interval quantities to maintain clarity and consistency. 4ths and 5ths are typically described as 'Perfect' because of their fundamental harmonic stability within a key. Conversely, 2nds, 3rds, 6ths, and 7ths are described using 'Major' or 'Minor' (or Augmented/Diminished) to reflect their more varied and often more colorful roles in melodic and harmonic contexts.

How does understanding enharmonics help me with identifying notes in chords on the guitar?

Understanding enharmonics is vital for correctly analyzing and naming notes within chords. For instance, in a C Major Sixth chord, the note 'A' is correctly identified as a Major Sixth from C. However, in a C Diminished Seventh chord, an enharmonically equivalent note (same fret on the guitar) would be spelled 'Bbb' to reflect its function as a Diminished Seventh from C. The accurate spelling, despite the same sound, is essential for understanding the chord's theoretical structure and function.

What is the recommended approach for a guitarist to correctly name an interval?

The most straightforward way to name an interval correctly is to first determine its quantity by counting the letter names of the notes in the major scale between the two pitches (e.g., C to D is a 2nd, C to E is a 3rd). Once you have the quantity, use the number of half-steps to identify the precise quality (Minor, Major, Perfect, Augmented, or Diminished) from a comprehensive interval chart. Focusing on counting the notes first simplifies the process.