Experimenting with the Melodic Minor Scale
Learn How To Create Chords And Modes From The Melodic Minor Scale
In this tutorial, we are going to have fun with a very particular kind of scale, the Melodic Minor scale.
You'll find the most common fretboard patterns for playing this scale up and down the neck, with root on the three lowest strings.
We'll also apply music theory to generate chords and modes from this scale, so let's begin!
Interactive Melodic Minor Scale Guitar Fretboard
Use this tool to see various ways to play the Melodic Minor scale on the guitar:
Melodic Minor Scale Fretboard Patterns
Here below are the most common ways to play this scale.
The examples provided are in the key of C, you can shift the shapes up or down the neck to play with another root.
Melodic Minor Scale - Fretboard Patterns
Melodic Minor Scale - Horizontal fretboard pattern
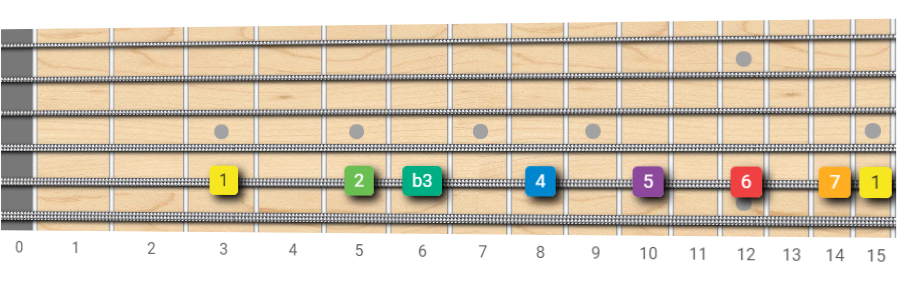
Melodic Minor Scale - Fretboard pattern with root on the 6th string
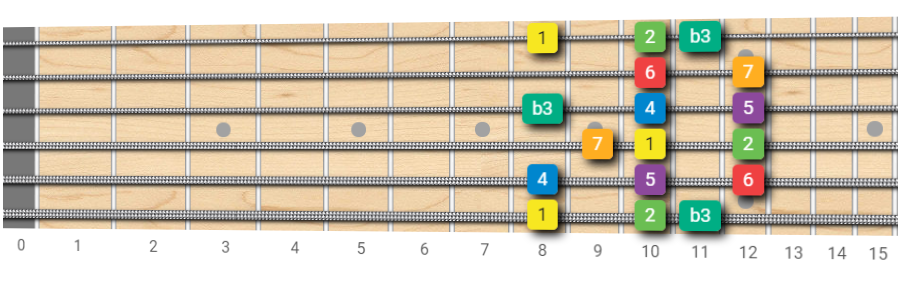
Melodic Minor Scale - Fretboard pattern with root on the 6th string - v2
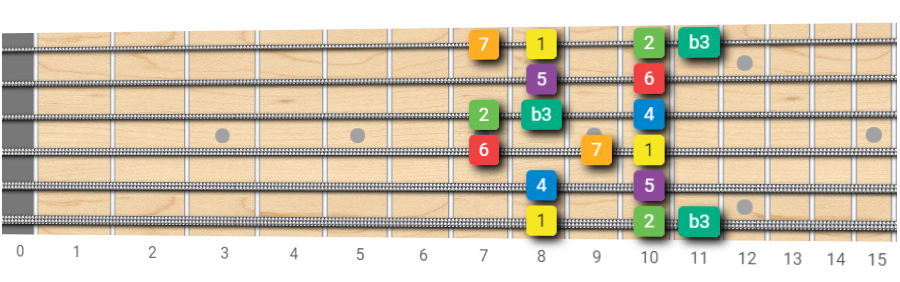
Melodic Minor Scale - Fretboard pattern with root on the 5th string
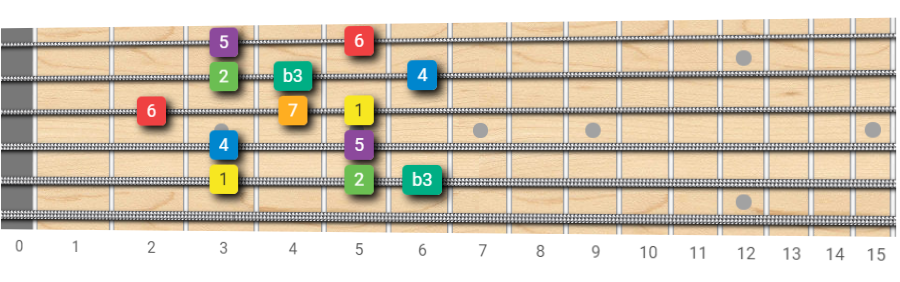
Melodic Minor Scale - Fretboard pattern with root on the 4th string

Melodic Minor Scale - Fretboard pattern with root on the 3rd string

You find more scale patterns across all the fretboard in my ebook Scales Over Chords | Learn How To Play The Right Scales Over Any Chord
Natural, Harmonic and Melodic Minor Scale Formulas
For a better understanding of minor scales, you should know that actually there exist 3 main types of minor scales:
- The Natural Minor Scale (also called Aeolian scale)
- The Harmonic Minor Scale
- The Melodic Minor Scale.
They have apparently subtle differences but with a great impact on the overall sound.
Natural Minor Scale
The Natural Minor scale is the relative minor of a major scale, this means that you can obtain a minor scale by playing all the notes in a major scale starting from its 6th degree instead from the root (A in the case of the C major scale).
Harmonic Minor Scale
If we raise the b7 of a natural minor scale by one half-step, it becomes a major seventh (7) and we get a Harmonic Minor scale.
I know what you are thinking: why the Harmonic Minor scale? Were the Natural Minor scale not enough?
This answer is going to be complicated, basically, the Harmonic Minor scale allows to use of a leading tone in a natural minor scale context.
You can safely ignore this stuff, just know that Mozart used this concept a lot.
Melodic Minor Scale
Do you see the big jump between the b6 and the 7 in the Harmonic Minor scale above?
In ancient times, some music theorists noticed that 3 half-steps (or semitones, or frets) were a too difficult distance to sing, so they decided to raise the b6 by one sharp (6): the Melodic Minor Scale was born.
Chords Created From the Melodic Minor Scales
Like for any other scale, we can generate chords from a scale by stacking its notes moving by third intervals.
Let's take as an example the A Minor Melodic Scale:

By stacking third intervals on any note of the scale, we obtain the following table:
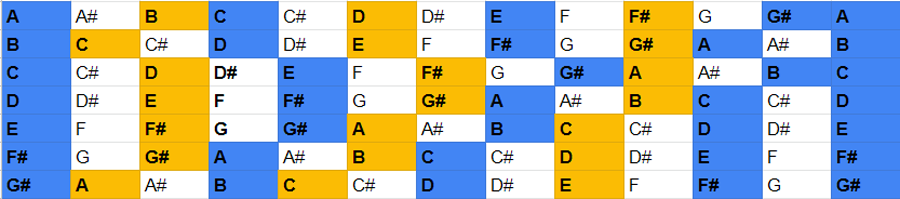
The cells in orange are the notes that belong to the A melodic minor scale (A, B, C, D, E, F#, G#); the cells in blue are the root and the thirds from that root: they are the tones in the chords.
Depending on the distances in semitones between the chord tones, we have different chord qualities. For example, take the first chord, composed of A, C, E and G#:

This chord in composed of the root, a Minor Third (3 half-steps from the root) denoted as b3, a Perfect Fifth (7 half-steps), denoted as 5 and a Major Seventh (11 half-steps), denoted as 7.
This is a Am(maj7) chord, a particular chord that is of minor quality, but with a Major Seventh!
If need help with intervals distances and names, check my freboard intervals tutorial.
If we repeat this process for all the notes in the melodic scale, we finally obtain all the chords in this scale:
| A m(maj7) | B m7 | C aug(maj7) | D 7 | E 7 | F# m7/b5 | G# m7/b5 |
|---|---|---|---|---|---|---|
| G# (7) E (5) C (b3) A (1) |
A (1) F# (6) D (4) B (2) |
B (2) G# (7) E (5) C (b3) |
C (b3) A (1) F# (6) D (4) |
D (4) B (2) G# (7) E (5) |
E (5) C (b3) A (1) F# (6) |
F# (6) D (4) B (2) G# (7) |
That's a strange scale with very particular chords, such as the A m(maj7) or the C aug(maj7).
Important: the chord construction process we have just seen, in which you stack thirds over any note in the scale, works exactly for all the scales. Yes, you can harmonize any type of scale with this process.
Modes Of The Melodic Minor Scale
Like with the modes of the Major Scale (Ionian, Dorian, Phrygian, Lydian, Mixolydian, Aeolian and Locrian) we can generate modes from the Melodic Minor scale by playing all the notes in that scale starting from any note.
Let's play the following note sequences:
- A, B, C, D, E, F#, G#, A: this is the A Melodic Minor scale
- B, C, D, E, F#, G#, A, B: this is the B Dorian B2 scale
- C, D, E, F#, G#, A, B, C: this is the C Lydian Augmented scale
- D, E, F#, G#, A, B, C, D: this is the D Lydian Dominant scale
- E, F#, G#, A, B, C, D, E: this is the E Mixolydian B6 scale
- F#, G#, A, B, C, D, E, F#: this is the F# Aeolian B5 scale
- G#, A, B, C, D, E, F#, G#: this is the G# Super Locrian scale
You find the fretboard diagrams for playing these scales over the entire fretboard in my complete ebook Scales Over Chords | Learn How To Play The Right Scales Over Any Chord.
Here's a recap table with the formula of the Modes of the Melodic Minor scale:
| Scale | Formula |
|---|---|
| Melodic Minor Scale |
1
b2
2
b3
3
4
b5
5
#5
6
b7
7
|
| Dorian B2 Scale |
1
b2
2
b3
3
4
b5
5
#5
6
b7
7
|
| Lydian Augmented Scale |
1
b2
2
b3
3
4
#4
5
#5
6
b7
7
|
| Lydian Dominant Scale |
1
b2
2
b3
3
4
#4
5
#5
6
b7
7
|
| Mixolydian B6 Scale |
1
b2
2
b3
3
4
b5
5
b6
6
b7
7
|
| Aeolian B5 Scale |
1
b2
2
b3
3
4
b5
5
b6
6
b7
7
|
| Super Locrian Scale |
1
b2
2
b3
3
4
b5
5
b6
6
b7
7
|
For further reference, here are a table showing the notes in the Melodic minor scale for every key:
| 1 | 2 | b3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| C | D | Eb | F | G | A | B |
| G | A | Bb | C | D | E | F# |
| D | E | F | G | A | B | C# |
| A | B | C | D | E | F# | G# |
| E | F# | G | A | B | C# | D# |
| B | C# | D | E | F# | G# | A# |
| F# | G# | A | B | C# | D# | E# |
| Gb | Ab | Bbb | Cb | Db | Eb | F |
| C# | D# | E | F# | G# | A# | B# |
| Db | Eb | Fb | Gb | Ab | Bb | C |
| G# | A# | B | C# | D# | E# | F## |
| Ab | Bb | Cb | Db | Eb | F | G |
| D# | E# | F# | G# | A# | B# | C## |
| Eb | F | Gb | Ab | Bb | C | D |
| A# | B# | C# | D# | E# | F## | G## |
| Bb | C | Db | Eb | F | G | A |
| F | G | Ab | Bb | C | D | E |
Melodic Minor Scale: Conclusion
We have just seen the formula of the Melodic Minor scale, how to create chords on it, and the modes generated from that scale. Now you have a new option for your solos and improvisation.
Be sure to check my complete ebook on guitar scale, and to play a bit with my interactive guitar scale finder tool, that allows you to experiment with any type of scale up and down the neck.
This ends our adventures in minor scales; to download the free guitar resources and to stay updated, subscribe here.